L'enseignement musical au Moyen Age
Par Jacques VIRET
Maître de conférences à l'Institut de Musicologie de Strasbourg
Article tiré du magazine "Chant Floral" N°45, 1985
Tout système éducatif reflète une certaine société, une certaine culture, et se donne comme finalité la réalisation d'un idéal humain qui est celui de cette société et de cette culture. Au Moyen Age - surtout le haut Moyen Age - la foi chrétienne représente le pôle autour duquel gravitent les institutions et les activités : aussi l'enseignement en général s'organise-t-il sur la base de la doctrine religieuse, de l'Écriture, des célébrations rituelles de la messe et de l'office, de telle sorte que les différentes branches du savoir convergent vers ces centres vitaux auxquels elles se subordonnent délibérément. Aux yeux des Pères de l'Église, qui ont modelé en profondeur la mentalité médiévale, le principal devoir de l'être humain est la louange divine, à elle doivent tendre tous ses efforts et toutes ses aspirations. Le christianisme apparaît donc comme l'axe essentiel de la culture médiévale en son ensemble, un second axe important étant constitué par l'héritage de l'antiquité gréco-latine : nous retrouvons ces deux lignes de force dans le domaine de l'art musical, avec les conflits qu'elles sont susceptibles de provoquer ici comme ailleurs.
Jusqu'à la fondation des premières universités, au début du 13e siècle, il n'existe guère d'établissements éducatifs indépendants de l'Église. Durant les tout premiers siècles du Moyen Age, à la sombre époque des grandes invasions, les monastères sont les seuls îlots de culture ; créés au 5e siècle en Occident, ils recueillent les enfants dès le très jeune âge et les préparent à la vie contemplative où la récitation communautaire des «heures» canoniales occupe la majeure partie de la journée et de la nuit. Ainsi en ira-t-il jusqu'à la fin du Moyen Age, quitte le cas échéant à dédoubler l'école monastique en une schola interior groupant les futurs moines, et une schola exterior ouverte aux jeunes gens qui se destinent au ministère séculier, voire à des laïcs. Cependant les clercs séculiers - prêtres des paroisses, chanoines des églises collégiales ou cathédrales - seront depuis le 6e siècle formés pour la plupart dans des écoles épiscopales, qui comme les écoles monastiques bénéficieront de l'impulsion communiquée aux lettres et aux arts par Charlemagne et son ministre Alcuin. Aux écoles épiscopales se rattachent celles que l'on appelle capitulaires car elles dépendent d'un chapitre, autrement dit du collège des clercs d'une paroisse non épiscopale ; dans les plus petites localités la responsabilité de l'instruction incombe au seul curé, lequel se borne d'ordinaire aux rudiments de la lecture et de l'écriture. Enfin au 13e siècle la croissance des villes suscite la création d'universités, là où des professeurs réputés attirent de nombreux étudiants venus de près ou de loin : il s'agit en fait de corporations vouées à la transmission du savoir, douées d'une relative autonomie par rapport aux autorités religieuses et civiles, et possédant en outre des statuts, une réglementation et un programme d'études qui font défaut aux autres établissements scolaires. Ces derniers n'en poursuivent pas moins leur existence, avec une prospérité variable d'un endroit et d'une époque à l'autre, mais sans grand changement au fil des siècles (1).

Franchinus Gafurius devant ses élèves, d'après une gravure sur bois de son traité De Harmonia musicorum instrumentorum opus (Milan, 15.18). On lit dans le phylactère une définition traditionnelle de l'harmonie comme accord des opposés (Harmonia est discordia concors).
«Viva voce» : la méthode du bourrage de crâne
Écoles monastiques, épiscopales et capitulaires : partout et toujours l'institution scolaire est en relation étroite avec l'Église, c'est-à-dire avec la liturgie. Et cette liturgie celle de l'office aussi bien que celle de la messe - revêt un aspect constamment chanté; dans un style plus ou moins orné comme dans les antiennes et répons, sur une mélodie simple comme dans les hymnes de l'office, ou selon le procédé de la cantillation, récitation musicalisée en usage pour les lectures et prières. De ce fait l'apprentissage du futur moine ou du futur clerc ne peut qu'accorder une large place à la musique, d'autant plus qu'on lui demande d'emblée de prendre une part active à la liturgie chantée, soit en tant que chantre dans une schola ou une maîtrise spécialement formée à l'exécution du chant liturgique, ou tout au moins comme lecteur à l'église, dans la salle capitulaire ou au réfectoire. En sa Regula canonicorum règlement codifié à l'intention de son chapitre Chrodegang, l'évêque de Metz sous Pépin le Bref, souhaite que certains clercs soient désignés pour apprendre aux novices le chant de la messe et de l'office selon la tradition romaine (2). Cette « romanisation» de la liturgie est alors une préoccupation majeure des souverains carolingiens, soucieux d'assurer l'unification religieuse du royaume sous l'égide de Rome. Aussi verra-t-on Charlemagne, dans son Admonitio generalis de 789, situer le chant au premier rang des matières à enseigner dans les écoles monastiques et épiscopales : «les psaumes, le solfège (notas), le chant» viennent avant le comput (calcul des fêtes mobiles dans le calendrier) et la grammaire (3).
Si les psaumes sont ici mentionnés en tête, c'est qu'ils constituent le livre par excellence de l'enseignement. Lorsqu'il apprend à écrire le jeune enfant s'essaie à copier des versets psalmiques, et ce sont eux aussi qu'il apprendra d'abord à lire. On attend de lui qu'il sache tout le psautier par coeur aussi rapidement que possible cette mémorisation nécessite en moyenne deux à trois années (4). Comme en outre la seule traduction admise de l'Écriture est latine, cela implique que l'élève se familiarise avec cette langue et avec sa prononciation correcte : la dictio - fait partie de l'enseignement élémentaire. Sitôt celle-ci acquise on passe à la lectio, lecture cantillée selon des principes et des règles stricts. Le débit s'effectue à partir d'une hauteur vocale moyenne, la «corde récitative», et s'abaisse sur les degrés mélodiques plus graves à la fin des phrases ou membres de phrases, selon des formules fixées par la tradition et qui correspondent aux diverses ponctuations conclusives, suspensives ou interrogatives. Ces formules ponctuantes étaient marquées sur le livre par autant de signes conventionnels (qui ont donné naissance à nos modernes signes de ponctuation) : il fallait les connaître exactement, ainsi que les règles de leur adaptation à l'accentuation des mots latins. Cela n'allait pas de soi pour un enfant de dix ou douze ans, même si le passage à lire publiquement lui était indiqué la veille et qu'il pouvait ainsi le préparer avec soin. II devait en outre surveiller son intonation, sa tenue corporelle, et s'efforcer de rendre son élocution expressive d'après le contenu du texte lu (5).
Mais il y avait bien mieux - ou bien pire que cette lecture modulée sur un petit nombre de formules simples. Nous voulons parler du répertoire orné du propre de la messe, que l'élève devait retenir de mémoire jusqu'à ce que Guy d'Arezzo, au 11e siècle, n'inventât un moyen de noter avec précision les intervalles mélodiques. Il existait, certes, une notation alphabétique où chaque note correspondait à une lettre, de sorte qu'il eût été possible de transcrire exactement les intervalles chantés ; mais cette notation n'a jamais été employée dans la pratique, sauf exceptions, et la notation neumatique courante depuis la fin du 9e siècle consignait sur le parchemin non pas les notes de la mélodie mais les mouvements de la main par lesquels le chef de choeur dessinait dans l'espace les inflexions de la courbe sonore, avec toutes les finesses de l'interprétation rythmique (chironomie). Cette notation ne pouvait donc servir que si l'on connaissait au préalable la mélodie : étant donné l'ampleur presque démesurée du répertoire de la messe - plusieurs centaines de chants - sa mémorisation supposait un véritable dressage, un labeur pénible et assidu tant pour le maître que pour l'élève. La méthode, appelée viva voce, «de vive voix», exigeait du maître qu'il répète plusieurs fois chaque élément de la mélodie, mot ou incise, à l'élève, puis que celui-ci reprenne à son tour les mêmes éléments jusqu'à ce que, dûment corrigé, il soit en mesure de chanter sans faute la mélodie entière. Ét-le même processus recommençait pour chaque chant : un véritable bourrage de crâne que J. Smits van Waesberghe compare au gavage d'une oie (6) !
Qui étaient donc ces enfants ou adolescents astreints à un apprentissage aussi ardu ? Ceux qui formaient les rangs de la schola cantorum, littéralement «collège des chantres», avec le double sens impliqué par le mot « collège» : un groupement d'individus liés par une fonction commune, et une maison d'éducation. La première schola, dont les plus anciens témoignagès sûrs remontent aux alentours de l'an 700 (7), a été fondée à Rome pour collaborer aux offices solennels célébrés par le pape et sa cour ; elle réunissait, autour de sept chantres adultes qui en avaient la responsabilité, un ensemble de jeunes garçons recrutés pour leurs dons vocaux et musicaux parmi les enfants abandonnés (coutume fréquente à cette époque, les parents n'étant souvent pas en mesure d'assumer matériellement l'entretien de leur progéniture) : ainsi trouvaient-ils logement et subsistance dans l'orphelinat édifié à cet effet. D'autres scholae verront le jour par la suite dans différentes villes de la chrétienté latine, formées alors par une équipe de «séminaristes» des écoles épiscopales ou canoniales. Cependant les nouvelles conditions sociales survenues à partir du 11e siècle amèneront un changement important : les scholae cantorum se sépareront des établissements d'enseignement et choisiront leur effectif, selon la coutume romaine primitive, parmi les enfants délaissés. D'où le nom de panistae qui leur sera parfois donné (du latin panis, le pain, c'est-à-dire «enfants gagnant leur pain en chantant»), outre ceux de chorales ou duodeni (les douze, chiffre sacré, mais le nombre des choristes variait en réalité entre cinq et vingt-cinq environ) (8). Telle est l'origine des maîtrises, qui furent souvent de véritables conservatoires avant la lettre et jouèrent un rôle essentiel dans la vie musicale jusqu'à la fin de l'Ancien Régime ; l'enseignement y était dispensé par un cantor et un magister, ce dernier surtout pour les matières de culture générale.

Pythagore étudie les proportions consonantes selon la série numérique 4, 6, 8, 9, 12, 16. Miniature du traité Theorica Musicae de Franchinus Gafurius (manuscrit du 15e siècle, Londres, British Museum, Add. 4913).
La participation de la schola à la liturgie de la messe eût dû normalement se réduire aux chants du type antiphonique, à savoir la psalmodie chorale des introïts, offertoires et communions. Et tel était vraisemblablement le cas jusqu'à la réorganisation dont on vient de parler : les chants les plus ornés, réponsgraduels, alléluias et traits - ceux qui appartiennent au genre mélismatique, caractérisé par de longues vocalises ou jubili revenaient à des chantres adultes, mieux aptes à en surmonter les grandes difficultés de mémorisation et d'exécution. Toutefois même ces chants, les plus difficiles de tous, en vinrent à être confiés aux chorales. D'une part les clercs du chapitre qui avaient la haute main sur eux trouvaient commode de se faciliter ainsi la tâche, estimant ce lourd surcroît de travail imposé aux choristes justifié par l'entretien matériel qu'ils leur fournissaient tant bien que mal (et souvent plus mal que bien). D'autre part la valeur mystique éminente que l'on attribuait traditionnellement aux jubili - on pensait qu'ils imitaient le chant des anges - semblait convenir particulièrement aux voix d'enfants, êtres purs et innocents (9).
Le solfège avant le solfège
Un musicologue actuel qui s'est penché sur la pédagogie musicale médiévale (10) en a souligné à juste titre l'aspect moderne : cela pourra surprendre après ce qu'on vient de rappeler. Mais si l'on fait abstraction des excès évidents propres au «gavage» auquel on soumettait les garçons des scholae, on concédera néanmoins que la méthode en' ellemême avait du bon. En effet, l'apprentissage du répertoire se faisait viva voce, de bouche à oreille, sans intermédiaire écrit, et cela pour la simple raison qu'un tel intermédiaire, c'est-àdire un livre qui eût permis de lire les chants avec précision, n'existait pas avant le l le siècle. Par la force des choses l'enseignement musical revêtait un caractère vivant qui ira s'atténuant à mesure que la notation se perfectionnera, jusqu'à l'époque moderne où le premier stade du solfège classique, de la «théorie» élémentaire, consistera dans l'étude fastidieuse des signes écrits. Au Moyen Age il en allait autrement : l'enfant se trouvait plongé dès le départ dans un bain de musique, de cette musique monodique modale qui était, ne l'oublions pas, celle du temps où il vivait. Lé répertoire des chants liturgiques lui parvenait comme un héritage dont l'origine restait proche, et non encore dénaturé par des siècles de décadence. On se rendait compte que l'assimilation de ce répertoire, d'un style et d'une facture hautement raffinés, postulait une préparation adéquate de l'oreille et du sentiment musical : préparation coutumière qui demeurera dans l'enseignement des maîtrises et en constituera l'un des côtés les plus bénéfiques.
Ainsi, dans le même temps où il apprenait à lire, à écrire et à compter, tout en fréquentant les offices journaliers de son église ou de son monastère, le jeune élève était initié par son maître de musique à ce que l'on appellera plus tard le solfège dans le meilleur sens du terme, celui d'une formation auditive. Cette formation consistait avant tout dans l'étude des intervalles musicaux, leur reconnaissance et leur justesse d'intonation, en se limitant d'abord à ceux que renferme la monodie grégorienne : secondes majeure et mineure, tierces majeure et mineure, quarte juste et quinte juste, à l'exclusion donc du triton, des sixtes, septièmes et octave, inexistantes dans la pratique (avec de rarissimes exceptions pour les sixtes) ; soit, en y ajoutant l'unisson, un total de sept intervalles. On étendra assez tôt la série par l'introduction de ces intervalles inusités, à commencer par l'octave, l'une des trois consonances de base avec la quarte et la quinte, pour arriver (vers les 12e-13e siècles) à un éventail de vingt-quatre intervalles en y incluant les redoublements compris dans les bornes d'une double octave (11).

Guy d'Arezzo (à gauche) enseigne la théorie du monocorde à l'évêque Théobald. Miniature du 12e siècle (Wien, Oesterreichische Nationalbibliothek, Cpv 51).
Un instrument était alors d'un précieux secours pour cet apprentissage du solfège, autant que l'est aujourd'hui notre piano pour le même usage il s'agit du monocorde, accessoire fondamental de la théorie musicale médiévale, et pas seulement pour l'enseignement du solfège comme on le verra. La fabrication de cet instrument, peu répandu en dehors de son emploi didactique, est des plus simples : une corde unique (d'où son nom) tendue sur une caisse de résonance rectangulaire, avec un chevalet mobile permettant de modifier la longueur de la corde vibrante, et par conséquent la hauteur du son produit par pincement de la corde. Sous cette dernière était en outre disposée une feuille de parchemin indiquant les endroits de la corde où il fallait placer le chevalet pour obtenir chaque note. L'échelle était diatonique (hormis si bémol, seule altération admise jusqu'au 13e siècle), et ses degrés correspondaient aux lettres de la notation alphabétique : A = la, B = si, C = do etc. L'élève pouvait dès lors émettre tel intervalle demandé, ou reconnaître celui que faisait entendre le maître ; il pouvait également vérifier l'intonation d'une mélodie à apprendre en jouant chacune de ses notes sur l'instrument.
Guy d'Arezzo, moine bénédictin de la première moitié du 11e siècle - il naquit peu avant l'an 1000 et mourut vers 1050 - est l'un des noms les plus glorieux de toute la pédagogie musicale ; ses inventions font de lui le créateur du solfège, au sens précis du terme, et l'un des plus grands théoriciens du Moyen Age. C'est semble-t-il à l'abbaye de Pomposa qu'il conçut dès sa jeunesse les plus fécondes d'entre elles : le perfectionnement de la notation sur portée et la méthode de solmisation par syllabes mnémoniques. Mais ces innovations heurtaient à tel point les habitudes ancrées que Guy fut contraint, sans doute pour cette raison, de quitter Pomposa. Il séjourna alors en divers lieux avant de trouver dans la personne de Théobald, l'évêque d'Arezzo, un protecteur influent grâce à qui il put poursuivre dans les meilleures conditions son activité pédagogique. Théobald le nomma professeur de chant et de musique à son école épiscopale, et lui fit rencontrer le pape Jean XIX (1024-1033) à qui Guy présentera sa méthode d'enseignement ainsi qu'un antiphonaire transcrit selon la nouvelle notation.
Cette notation se singularisait non tant par le recours à la portée - le principe en était déjà connu auparavant, comme en témoigne notamment au 9e siècle le traité d'Ogier de Laon Musica enchiriadis (12) - que par la manière dont elle était employée. Guy eut en effet l'idée, simple mais géniale, d'échelonner les lignes non pas comme jusqu'alors en secondes mais en tierces, et de placer les notes tantôt entre les lignes, tantôt sur elles. Quatre lignes suffiront désormais pour noter les mélodies liturgiques, et des couleurs différentes, jointes aux clefs, rendront plus aisée la distinction des tons et demitons. On imagine la révolution qu'amena l'introduction de ce système : la mélodie pouvait ainsi être déchiffrée ou remémorée sans le secours de l'enseignement oral. Il en résulta un allégement considérable de l'effort de mémorisation requis des chorale, : à en croire Guy la durée d'apprentissage avait passé de dix à deux années (13) !
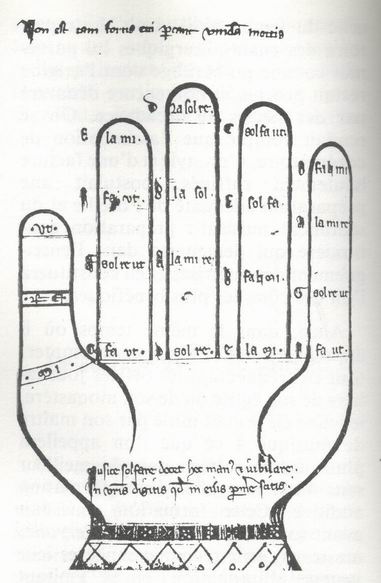
La «main guidonienne» d'après un manuscrit du 14e siècle (Londres, British Museum, Add. 1814?). Traduction des vers écrits au bas de la figure : «Cette main enseigne à solfier et à chanter selon l'art musical ; vos doigts vous montrent ce que vous aurez toujours à chanter».
Quant à la méthode de solmisation, chacun sait que Guy la créa d'après l'hymne à Saint Jean-Baptiste Ut queant laxis, dont la mélodie (14) - probablement composée ou tout au moins adaptée par lui - fait commencer chaque membre de phrase par l'une des six notes de l'hexacorde ascendant dola. Pourquoi, se demandera-t-on, éliminer la note si qui ne recevra son nom qu'au 17e siècle ? Sans doute parce que c'est une note mobile et que l'intention véritable de Guy consiste à créer une sorte de réflexe conditionné : en appliquant à chaque note d'une mélodie une syllabe conventionnelle, l'élève apprend automatiquement à rattacher cette note à la structure organique de l'échelle diatonique avec son alternance irrégulière de tons et demi-tons. Selon la théorie des «muances» hexacordales (15), non formulée explicitement par Guy mais codifiée un demi-siècle après sa mort par des traités qui lui en attribuent la paternité (16), l'hexacorde «naturel» do-la se transpose à la quinte (hexacorde «par bécarre») et, moyennant bémolisation du si, à la quarte aiguë (hexacorde «par bémol») sans que l'on change la syllabe assignée à chaque note. Ainsi le demi-ton se solfie toujours mi fa quelle que soit la hauteur à laquelle il se rencontre (mi fa, la - si bémol, si - do), à condition de pratiquer correctement les transpositions ou muances hexacordales. Dans l'esprit de Guy cette méthode était davantage qu'un simple procédé mnémotechnique permettant de localiser la place des demi-tons dans l'échelle diatonique : il s'agissait aussi et surtout d'un moyen de formation auditive, susceptible d'améliorer le sentiment musical de l'élève en créant en lui une conscience plus nette des intervalles mélodiques ; l'utilité immédiate, et pour ainsi dire mécanique, du procédé passe alors au second plan et c'est la raison pour laquelle Guy n'en fait point état lorqu'il relate son invention de la solmisation (17). Et il y a plus curieux : les six syllabes guidoniennes (de ut à la) entrent dans la composition d'un cryptogramme ésotérique sans rapport apparent avec la musique et dont l'agencement remonte à Paul Diacre, l'auteur du poème de l'hymne (9e siècle), à moins que celui-ci ne l'ait lui-même hérité d'une tradition plus ancienne (18). Il se révèle très diffcile sinon impossible de savoir avec certitude si ce cryptogramme revêtait ou non à l'origine une signification musicale implicite (19) ; Guy le connaissait très probablement, sinon pourquoi aurait-il retenu ce poème de préférence à d'autres qui eussent aussi bien convenu ? Quoi qu'il en soit les origines de la solmisation, on le voit, ne sont point aussi évidentes qu'il y parait. D'autre part il n'est pas sûr que la fameuse «main guidonienne», artifice pédagogique appliqué à l'entrainement de cette même solmisation, soit réellement une invention de Guy à qui on en a fait honneur dès le début du 12e siècle (20). De toute manière cette invention était peu originale puisque de longue date la main était utilisée dans l'enseignement comme accessoire mnémotechnique, par exemple pour apprendre le comput pascal (21). En pédagogie musicale on associe chaque jointure et phalange de la main gauche à l'une des vingt notes de la théorie (de sol 1 à mi 4), en désignant celles-ci conjointement par les lettres alphabétiques et les syllabes de solmisation, de sorte que la main droite peut indiquer sur la gauche telle note à faire chanter ou reconnaître par l'élève. D'innombrables traités reproduisent la < main guidonienne» jusqu'au 17e siècle, et attestent la très grande diffusion de ce procédé dans la pédagogie musicale du Moyen Age et de la Renaissance (22).
Il reste à parler d'une invention plus originale, et authentique celle-là, la méthode de composition mélodique à partir des voyelles d'un texte (23). jeu : on recopie les vingt notes de «jeu» : on recopie les vingt notes de la théorie en leur faisant correspondre dans l'ordre, et autant de fois qu'il le faut, les cinq voyelles de l'alphabet (A - E - I - O - U) ; puis l'on prend au hasard un texte latin quelconque, dont chaque syllabe engendrera une note d'après le tableau ainsi dressé. Il arrive alors que le résultat soit musicalement satisfaisant, comme par exemple pour le membre de phrase Sancte Johannes meritorum tuorum copias (do - ré - fa - do - ré etc.). Il arrive aussi que la mélodie obtenue soit mauvaise, auquel cas on lui apportera un correctif en décalant la correspondance notes-voyelles et en choisissant librement, pour chaque syllabe, entre les deux notes proposées par l'une et l'autre correspondance. L'exercice fait alors appel au sens musical de l'élève en lui demandant de juger par lui-même la valeur mélodique de sa réalisation. Rien n'empêche de reprendre de nos jours cette méthode ingénieuse en l'adaptant au français ou à une autre langue vivante.
De la pratique à la spéculation
L'une des singularités les plus surprenantes de la doctrine musicale médiévale réside dans son fort penchant à l'abstraction, à la spéculation ; c'est là une orientation qui la situe aux antipodes de nos conceptions modernes, conceptions qu'à d'autres égards elle préfigure comme on l'a vu. Pour le Moyen Age la musique a été d'abord une science avant d'être une pratique, de même que dans l'Antiquité pour les adeptes du pythagorisme. Nous avons affaire à un puissant courant de pensée qui, parti de la Grèce antique, parcourt tout le Moyen Age et au-delà, et assigne à la musique la valeur d'une véritable représentation du monde - universmacrocosme et hommemicrocosme dans la mesure où les intervalles musicaux rendent audibles, de par les rapports numériques qui les soustendent, l'harmonie cosmique fondée sur l'omnipotence du Nombre souverain. C'est dans ce sens qu'il convient d'interpréter les dernières paroles prononcées par Pythagore, selon la légende, au moment de mourir : «travaillez le monocorde ! ». En spéculant sur les proportions numériques des sons on pénètre ainsi l'ordre transcendant de toute réalité, le principe éternel et divin de l'harmonie universelle. C'est du même coup reléguer à un rang inférieur la musique pratique, perçue par l'oreille, pour exalter la musique rationnelle des nombres que seul l'entendement est en mesure d'appréhender. Et l'on justifie l'emprunt d'une doctrine païenne en invoquant le verset du livre de la Sagesse (11,21) d'après lequel Dieu a créé le monde selon «la mesure, le nombre et le poids». Ainsi penseront tous les théoriciens médiévaux, depuis Boèce dont le traité d'inspiration intégralement pythagoricienne représente pour eux l'autorité souveraine et incontestée en la matière. Même Guy d'Arezzo, pourtant si proche de la pratique et si plein de bon sens, n'hésitera pas à écrire au début de ses Regulae rhythmicae les vers bien connus : Musicorum et cantorum magna est distantia, isti dicunt, illi sciunt, quae componit musica. Nam qui facit, quod non sapit, diffinitur bestia («Grande est la distance entre musiciens et chanteurs ceux-ci chantent, ceux-là savent ce qui constitue la musique. Car celui qui fait cc qu'il ne comprend pas, on l'appelle une bête») (24). Il y a donc d'un côté le cantor (entendons : le praticien, c'est-à-dire aussi l'instrumentiste), qui connaît la musique par instinct ou par apprentissage empirique, et il y a de l'autre le musicus, le musicien à proprement parler, qui seul possède la science rationnelle des sons, celle notamment des rapports numériques d'intervalles et des proportions arithmétiques dont. l'étude est l'objet essentiel de la science pythagoricienne. Entre les deux disciplinés, la musica practica et la musica speculativa, se dresse une barrière solide peu nombreux sont ceux qui s'adonnent en même temps à l'une et à l'autre. Par ailleurs, la pratique d'exécution tend à acquérir un caractère de plus en plus rationalisé, parallèlement aux progrès de la notation : au 14e siècle apparaît le système dit proportionnel, indiquant avec une précision nouvelle les durées rythmiques grâce à un arsenal complexe de signes et de conventions graphiques. L'iconographie montre que même les enfants des maîtrises chantent «sur le livre», ce qui laisse supposer qu'ils doivent se familiariser très tôt avec les arcanes de la notation proportionnelle, à moins que leur mémoire auditive ne vienne opportunément aplanir les difficultés de cette lecture. D'après Guillaume de Van (25) la gymnastique mentale nécessaire pour déchiffrer la musique polyphonique du bas Moyen-Age dépasserait son utilité pratique elle aurait entouré l'exercice de la musique savante d'un certain ésotérisme, pour le réserver à une élite d'initiés dont l'esprit s'est affiné au contact des nombres et de leurs combinaisons. Certains manuscrits seraient même sciemment conçus en vue de développer ce genre de facultés, par la multiplication des problèmes de lecture rythmique.
Hormis ce cas particulier la progression des études musicales s'efforce de suivre à peu près les étapes de l'évolution psychologique de l'enfant. C'est ainsi qu'après la première formation surtout pratique - mémorisation du répertoire, solfège élémentaire - le passage à l'adolescence lui permettra d'accéder aux aspects spéculatifs de la musique. Son intelligence se perfectionne de même que son sens de l'abstraction, et il peut dès lors aborder avec succès l'étude des septs arts libéraux, ces disciplines de base que depuis le début du Moyen Age on subdivise traditionnellement en trivium et quadrivium : le trivium groupe les trois matières littéraires, grammaire, rhétorique, dialectique, tandis que le quadrivium réunit les quatre branches tributaires du nombre, arithmétique, géométrie, musique et astronomie. Boèce, fervent pythagoricien, avait projeté de consacrer un traité à chacune des disciplines du quadrivium, mais il ne put achever que deux d'entre eux, le De institutione musica et le De institutione arithmetica. Les deux exposés se recoupent en partie, et cette similitude prouve éloquemment à quel point la science musicale pythagoricienne - et par voie de conséquence la doctrine musicale médiévale en son ensemble - rejoint la science des nombres. Relisons Cassiodore, autre auteur de référence : «La musique est la discipline ou la science qui traite des nombres dans leurs rapports» (quid ad aliquid sunt) (26). Ce qu'Aurélien de Réomé, théoricien de l'époque carolingienne, explicite comme suit «(La musique) embrasse cette partie du nombre qui consiste dans le rapport (quae ad aliquid refertur), comme celui du simple au double ou au triple, ou un quelconque autre semblable» (27). Ainsi le substrat de la musique, selon la pensée médiévale façonnée par le pythagorisme, réside non tant dans le nombre en soi que dans les relations des nombres entre eux, ce qui conduit aux notions apparentées de proportion et proportionnalité, la proportion établissant une relation entre deux nombres, la proportionnalité entre deux proportions (28).
Pour se familiariser avec ces notions arithmético-musicales l'élève continue à se servir du monocorde, mais il le considère alors sous une autre optique. Au. lieu de se fier aux lettres qui sur la feuille de parchemin lui signalent l'endroit de la corde à appuyer pour obtenir le son correspondant, il doit maintenant mesurer les longueurs de la corde délimitées par chaque note de l'échelle ; il peut ainsi vérifier de visu et de auditu que le degré de consonance de l'intervalle produit va de pair avec la simplicité du rapport numérique entre la longueur totale de la corde et la fraction de celle-ci permettant de jouer l'octave, la quinte ou la quarte. Le rapport de ces trois intervalles, les «consonances parfaites», est en effet respectivement 1/2, 2/3 et 3/4, ce qui signifie qu'il faut appuyer la corde à la moitié, aux deux tiers et aux trois quarts de sa longueur pour les obtenir. Et l'on s'émerveille de constater que ces rapports consonants font exclusivement intervenir les nombres 1, 2, 3 et 4, soit la fameuse tétraktys. pythagoricienne dont la somme donne le nombre parfait de 10. La tétraktys passe pour la matrice du monde animé et inanimé, de sorte que l'étude des consonances musicales qui en sont une admirable manifestation est censée dévoiler l'ordre transcendant de l'univers, cette harmonie intelligible transformant la diversité des phénomènes en un cosmos unifié par la cohérence des nombres créateurs. On consent néanmoins à franchir les bornes de la sainte tétraktys pour introduire dans la série les chiffres 8 et 9 figurant dans le rapport de la seconde majeure, différence entre la quinte et la quarte. Afin de ramener les quatre intervalles à une constellation numérique minimale on établit la série 6, 8, 9, 12 où l'octave, la quinte, la quarte et le ton entier sont figurés par les rapports respectifs 6/12, 6/9 ou 8/12, 6/8 ou 9/12 et 8/9. Cette série 6,8,9,12, qui pouvait s'amplifier en 4, 6, 8, 9, 12, 16, exerça une véritable fascination sur les artistes médiévaux : ils s'en servirent pour le plan de maintes oeuvres picturales ou architecturales, et cela jusqu'à la Renaissance inclusivement on la rencontre entre autres chez Raphaël, Botticelli, Mantegna, Ghirlandajo, Benozzo Gozzoli, Léonard de Vinci, Albert Dürer, et l'humaniste et architecte Léon-Battista Alberti préconise de calculer les proportions architecturales d'après les nombres «musicaux» (voir son traité De re aedificatoria, 1485) (29). On est en droit de .présumer que la même série numérique régit l'agencement structural de nombreuses oeuvres musicales médiévales ou renaissantes, mais cette question a encore été peu étudiée jusqu'à présent.
L'octave, la quinte, la quarte et le ton entier ne représentent que le début et la partie la plus simple de la musica speculativa ou arithmetica, déduite directement des mensurations monocordales. Il n'en va plus de même dès qu'on aborde les autres intervalles diatoniques, demi-ton, tierces, triton, sixtes et septièmes : on pénètre alors dans le domaine de la véritable spéculation, c'est-à-dire du calcul dépassant les bornes de l'expérimentation. Ainsi pour obtenir le rapport de la tierce majeure pythagoricienne, formée par l'addition de deux tons entiers, il faut multiplier la fraction 9/8 par elle-même, ce qui donne 81/64 (le 'rapport simple de la tierce harmonique, 5/4, ne sera pas admis avant Zarlino au 16e siècle). Et la complication s'accroît considérablement lorsqu'il s'agit de chiffrer un intervalle tel que le demiton chromatique compris entre si bémol et si bécarre, pour lequel on obtient 2187/2087 ; ou plus encore, si l'on s'avise d'évaluer le «comma pythagoricien» séparant l'octave et l'addition de six tons entiers (ou, plus précisément, celle de six quintes ascendantes et six quartes descendantes) ; on arrive ici à la proportion 531441/ 524288 (30):
De telles élucubrations, fort éloignées de la musique vivante, proviennent en droite ligne du pythagorisme antique dont le Moyen Age a eu connaissance par l'intermédiaire de Boèce. Ce dernier, quoique ayant vécu au début du 5e siècle, ignore totalement la musique chrétienne de son temps pour n'accorder son attention qu'à la théorie grecque qui déjà alors fait figure d'héritage caduc. Caduc à plus forte raison pour les étudiants du Moyen Age qui devront à cause de Boèce encombrer leur mémoire, bien vainement, des noms de notes jadis attribués aux cordes de la lyre dans le systema teleion : « paranète des hyperbolées», «hypate des hypates», etc . Ils devront aussi, toujours selon Boèce, calculer les proportions des trois «genres», diatonique, chromatique et enharmonique, soit par exemple pour ce dernier: 2304, 2916, 2994, 3072. Mais tous n'ont pas les capacités de s'aventurer jusque-là : Guy d'Arezzo qualifie cette spéculation de «très ardue» (difficillimam) (31) et il reconnaît qu'elle s'adresse plutôt aux philosophi qu'aux cantores (32)...
Lors de la fondation des premières universités, au début du 13e siècle, la science musicale prendra naturellement place, aux côtés des autres disciplines du trivium et du quadrivium, parmi les matières enseignées à la «faculté des arts». Cette faculté est propédeutique : il faut la fréquenter pour obtenir, vers dix-neuf ou vingt ans, le baccalauréat qui ouvre l'accès aux facultés supérieures de théologie, droit et médecine, à moins qu'on ne pousse plus loin l'étude des mêmes «arts». Cependant l'importance dévolue aux sept disciplines apparaît très inégale : on met l'accent principalement sur la grammaire (latine) et la dialectique, pour ne consacrer à la musique, la plupart du temps, que trois ou quatre semaines (33). Il y a pourtant lieu de croire qu'à Paris la musique était mieux servie, en accord avec le rayonnement de cette cité comme centre musical depuis l'«école de Notre-Dame» aux 12e-13e siècles. Et il semble bien que l'enseignement musical dispensé à la primitive Sorbonne ne revêtait pas un caractère uniquement spéculatif : c'est très certainement dans ses murs que le trouvère artésien Adam de la Halle, vers 1270, s'initia à la technique polyphonique qu'il fut ensuite le premier à appliquer à des compositions profanes, ses célèbres rondeaux à trois voix. Au siècle suivant la Sorbonne comptera au nombre de ses professeurs les plus en vue Johannes de Muris (ou Jean de Murs), également versé dans les quatre sciences du quadrivium et connu autant comme astronome et mathématicien que comme musicien : le pape Clément VI le consulte en 1344 au sujet de la réforme du calendrier.

Psaume 25 avec signes de ponctuation mélodique, d'après un psautier manuscrit du 10° siècle (Stuttgart, Württembergische Landesbibliothek, Cod. bibl.).
Auteur de plusieurs volumineux traités qui seront les manuels officiels de l'enseignement universitaire de la musique jusqu'à la fin du 15e siècle, Johannes de Muris contribue avec Philippe de Vitry à mettre au point les principes de la notation proportionnelle, qu'il relie à des considérations d'ordre mathématique et astronomique. Il fait école, comme le prouvent plusieurs traités rédigés par ses disciples d'après son enseignement (34).
En marge des universités qui se fondent peu à peu dans les villes culturellement les plus florissantes, les écoles épiscopales et monastiques, dirigées par un écolâtre qui nomme les professeurs, continuent à dispenser un enseignement de caractère plus pratique, où le chant voisine avec le comput, la grammaire, la dialectique et la théologie. A l'étude du cantus planus, le chant monodique «plane» (c'est-àdire non mesuré), et du cantus mensuratus, le chant polyphone mesuré écrit en notation proportionnelle, s'ajoutent celle de la solmisation hexacordale au moyen de la «main guidonienne» et celle de l'octoéchos, c'est-àdire des huit modes grégoriens. Pour familiariser l'élève avec chaque mode on lui fait retenir de brèves mélodies qui en résument la structure, anciennement sur des syllabes dépourvues de sens (noeanoeane pour les authentes, noeagis pour les plagaux), puis plus tard sur des paroles empruntées à l'Écriture (Primum quaerite regnum Dei, etc.). Ainsi il peut choisir correctement le ton psalmodique convenant à chaque antienne, en fonction de la teneur et de la finale de celle-ci, c'est-à-dire de sa dominante et de sa tonique modales. Ici aussi la spéculation intervient en cherchant à rattacher arbitrairement les modes grégoriens aux tons de la Grèce antique énumérés par Boèce : depuis le 9e siècle l'authente de ré s'appellera le dorien, son plagal l'hypodorien, etc. Et l'on en viendra, moyennant de multiples «truquages», à définir la structure des modes selon une symétrie factice leur ambitus commun sera fixé à l'octave, partagée en quinte et quarte pour les authentes et en quarte et quinte pour les plagaux ; telle est la théorie modale hybride et artificielle que répandront couramment les traités depuis le 10e siècle (35).
Nous ne saurions clore ce panorama très général de l'enseignement musical du Moyen Age sans rappeler que les écoles n'ont pas été le seul lieu d'apprentissage de la musique. II ne faut pas oublier en effet la cohorte des musiciens profanes, jongleurs et ménestrels, qui apprennent leur art «sur le tas», par échanges et contacts mutuels lors des rassemblements tenus à dates régulières, d'ordinaire en période de Carême où tout divertissement profane est interdit (36). Jongleurs et ménestrels cultivent, en plus du chant lyrique ou épique dont ils sont les propagateurs, l'art instrumental, celui de la vièle en particulier, qui restera jusqu'à la fin du Moyen Age leur apanage sinon leur monopole exclusif : les musiciens savants ne dédaignent pas, à l'occasion, de se récréer en touchant quelque instrument bien que cette pratique soit placée au rang le plus bas dans la hiérarchie des valeurs musicales. Cela changera à l'époque de la Renaissance, de pair avec l'ensemble des conceptions relatives à la musique : la «science musicale» perdra son caractère purement spéculatif, et la musica practica s'en trouvera d'autant valorisée, tandis que l'invention de l'imprimerie viendra bouleverser, ici comme ailleurs, les activités intellectuelles et culturelles. Une nouvelle ère commence, celle de l'humanisme, et les bases sont dès lors jetées d'un monde transformé qui est, encore le nôtre.
(1) Sur l'enseignement et les écoles au Moyen Age, voir les contributions de Pierre Riché et Jacques Verger à l'Histoire mondiale de l'éducation, t. 1, Paris, P.U.F., 1981, pp. 215-244 et 281-309. (Retour)
(2) Chrodegang, Regula canonicorum, chap. L ; dans Migne, Patrologie latine, 89, col. 1079 Constituantur interea seniores fratres... qui tempore statuto vicissim cum cantorum schola sint ; la mention de la schola cantorum renvoie implicitement aux usages romains. (Retour)
(3) Monumenta Germaniae historica ; Capitularia regum francorum, t. 1, p. 60 : «Psalmos, notas, cantus, compotum, grammaticam per singula monasteria vel episcopia» (il faut ajouter sans doute doceri manquant dans le texte conservé). (Retour)
(4) D'après Joseph Smits van Waesberghe, Lehre und Theorie der Musik im Mittelalter (Musikgeschichte in Bildern, 111/3), Leipzig, Veb Deutscher Verlag für Musik, 1969, p. 23. (Retour)
(5) Ces prescriptions sont données par plusieurs auteurs médiévaux, notamment par Alcuin et son disciple Raban Maur. Cf. Smits van Waesberghe, op. cit., pp. 70-71. (Retour)
(6) Ibid., p. 25. (Retour)
(7) Cf. Solange Corbin, L'Église à la conquête de sa musique, Paris, Gallimard, p. 182. (Retour)
(8) Cf. Smits van Waesberghe, op. cit., p. 16. (Retour)
(9) Ibid., p. 25. (Retour)
(10) Georges Favre, Histoire de l'éducation musicale, Paris, La Pensée Universelle, 1980, pp. 42-43. (Retour)
(11) Smits van Waesberghe, op. cit., p. 76. (Retour)
(12) Martin Gerbert Scriplores ecclesiastici de musica sacra .... Saint-Blaise, 1784, t. I, pp. 156 sqq. (Retour)
(13) Epistola Michaeli monacho, dans Gerbert, Scriptores, 11, p. 43. (Retour)
(14) Antiphonaire monastique, Solesmes, 1934, p. 922. (Retour)
(15) Sur la solmisation hexacordale, voir Jacques Chailley, La musique et le signe, Lausanne, éd. Rencontre, 1967, pp. 38 sqq. (Retour)
(16) Cf. Smits van Waesberghe, op. cit., p. 116. (Retour)
(17) Epistola..., p. 45. Cf. Smits van Waesberghe, op. cit., p. 112. Dans le Micrologus de musica (chap. VII-VIII, Gerbert, Scriptores, II, pp. 8-9 ; éd. Smits van Waesberghe, American Intitute of Musicology, 1955, pp. 117-129) Guy explique que les divers polycordes peuvent se transposer d'une région de l'échelle à l'autre, sans établir de rapprochement avec l'emploi des syllabes de solmisation ; d'autre part l'Epistola ne -mentionne pas la transposition possible des syllabes de solmisation. (Retour)
(18) Ce cryptogramme a été découvert par nous-même et présenté dans notre thèse sur La figuration mélodique du chant grégorien, soutenue à Paris-Sorbonne en février 1981. Notre directeur de recherches, M. Jacques Chailley, en a complété l'explication ; voir son article «Ut queant laxis et les Origines de la Gamme», dans Acta Musicologica, LVI, 1984/1, pp. 48-69. (Retour)
(19) Voir le chapitre VI de notre ouvrage Le chant grégorien, musique de la parole sacrée, Lausanne, éd. L'Age d'Homme, sous presse. (Retour)
(20) Cf. Smits van Waesberghe, op. cit., p. 120. (Retour)
(21) Ibid. (Retour)
(22) Ibid., pp. 124-143. (Retour)
(23) Micrologus de arte musica, chap. XVII, dans Gerbert, Scriptores, II, pp. 19-21 ; éd. Smits van Waesberghe, pp. 186-195. Cf. Smits van Waesberghe, op. cit., pp. 114-115. (Retour)
(24) Regulae rhythmicae, dans Gerbert, Scriptores, 11, p. 25. (Retour)
(25) «La pédagogie musicale à la fin du Moyen Age>>, dans Musica disciplina, 11, 1948, pp. 75-97. (Retour)
(26) Gerbert, Scriptores, 1, p. 16. (Retour)
(27) Ibid, p. 35. (Retour)
(28) La théorie des proportionnalités s'applique à la recherche des moyennes ou médiétés, ce qui sur le plan musical équivaut au partage d'un grand intervalle en deux plus petits, spécialement de l'octave en quarte et quinte (moyenne arithmétique, par exemple 9 pour 6 et 12) ou en quinte et quarte (moyenne harmonique, par exemple 8 pour 6 et 12). Voir à ce sujet Jacques Chailley, Expliquer l'harmonie ?, Lausanne, éd. Rencontre, 1967, pp. 22 sqq. (Retour)
(29) Cf. Smits van Waesberghe op. cit., pp. 66-67. (Retour)
(30) Ibid., p. 36. (Retour)
(31) Micrologus, chap. XX, dans Gerbert, Scriptores, II, p. 24. (Retour)
(32) Epistola..., dans Gerbert, II, p. 50. (Retour)
(33) Sur l'enseignement musical dans les universités médiévales, cf. Peter Wagner, Universität und Musikwissenschaft, Fribourg (Suisse), 1921, pp. 14 sqq. ; et N. Carpenter, Music in the Medieval and Renaissance Universities, Norman (Oklahoma), 1958. (Retour)
(34) Trois traités secundum Johannem de Muris ont été édités par Charles E.H. de Coussemaker dans le troisième tome de ses Scriptores : ils exposent respectivement le chant mesuré (Libellus cantus mensurabilis..., pp. 46-58), .le contrepoint (Ars contrapuncli..., pp. 59-68) et le déchant (Ars discantus..., pp. 68-113). (Retour)
(35) Voir à ce sujet Jacques Chailley, L'imbroglio des modes, Paris, Leduc, 1960. (Retour)
(36) Cf. Théodore Gérold, La musique au Moyen Age, Paris, Champion, 1932, p. 367. (Retour)
Retour




